Представата на човека за движението на планетите е претърпяла дълго развитие. В древността се е считало, че Земята е център на Вселената, а Слънцето и звездите обикалят около нея. Наблюденията на движение на небесните тела, обаче не съвпадали с тази представа.
Йохан Кеплер (1571 – 1630 г.) е германски математик, астроном и астролог. Кеплер живее във време, в което още няма ясна граница между астрономия и астрология. Той е ключова фигура в Научната революция с изведените от него закони за движението на планетите.
Неговите трудове стават основа за теорията на Исак Нютон за всеобщото привличане.

Йохан Кеплер – портрет от 1610г.
В своята кариера Кеплер е учител по математика в Грац, след това е асистент на астронома Тихо Брахе и накрая императорски математик на Рудолф II и неговите наследници. Освен това преподава математика в университета в Линц. Той има значителен принос в оптиката, като създава и подобрен вариант на рефракторния телескоп.
Интересът към астрономията идва у Кеплер още като дете - през 1577г. майка му му показва преминаващата по това време ярка комета, а след три години и лунно затъмнение. В същото време прекарано заболяване от едра шарка го оставя с влошено зрение и осакатени ръце, което през целия му живот е пречка за извършване на астрономически наблюдения.

Голямата комета от 1577г., наблюдавана прецизно от Тихо Брахе.
През 1591 постъпва в Университета в Тюбинген - първо във Факултета по изкуствата, сред които по това време са били и астрономията, и математиката, а след това отива в Богословския факултет. Тук за първи път чува за хелиоцентричната система на Николай Коперник и веднага ѝ става твърд поддръжник.
През 1604 г. Кеплер публикува своите наблюдения на свръхнова, наречена сега на неговото име. От тогава в нашата галактика свръхнови, видими с невъоръжено око, не са наблюдавани.
На базата на систематичните и точни астрономически наблюдения на Тихо Брахе, Кеплер извежда първите два закона за движението на планетите, които публикува в книгата си "Новата астрономия" през 1609г. Опасявайки се да дава категорични изводи, първоначално той определя, че законите му се отнасят само до Марс.
През 1610г. Галилей съобщава на Кеплер за откриването на спътниците на Юпитер. Кеплер първоначално се отнася недоверчиво, докато не получава свой собствен телескоп, и сам наблюдава спътниците. Това го кара да се заеме с теорията на лещите, усъвършенства телескопа и издава фундаменталния си труд "Диоптрика".
По-късно, през 1618 г. Кеплер формулира третия си закон и вече не като отнасящ се само за Марс, но и за всички други планети (включително, разбира се, и Земята), както и галилеевите спътници. Резултатите Кеплер публикува в книгата си "Хармонията на света".
I. Закон на Кеплер.
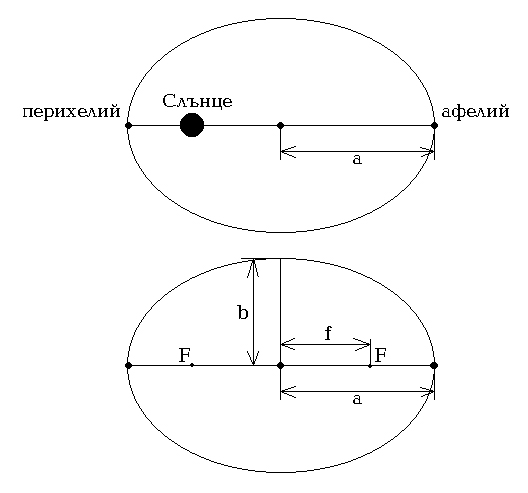
Планетите се движат около Слънцето по елипси, в единия от фокусите на които се намира самото Слънце.
a - голяма полуос на елипсата b - малка полуос на елипсата f - фокусно разстояние, а т.F – фокуси на елипсата
Основно свойство на елипсата: Сумата от разстоянията от всяка точка на елипсата до двата фокуса е постоянна величина - равна на 2a.
Ексцентрицитетът на елипсата е:
e = 𝑓𝑎 = √𝑎2−𝑏2𝑎
Когато e = 0, елипсата става окръжност с радиус r = a = b, а когато e = 1, елипсата се сплесква до отсечка с дължина 2a.
Разстоянието от Слънцето до планетата в перихелий (най-малко разстояние) е:
rп = a - f = a.(1 - e) ,
а разстоянието в афелий (най-голямо разстояние):
rа = a + f = a.(1 + e)

II. Закон на Кеплер.
Планетите се движат по орбитите си неравномерно. За равни интервали от време радиус-векторът на планетата описва равни по големина площи от орбитата. Δt1, Δt2 - интервали от време S1, S2 - описвани площи Ако Δt1 = Δt2, то S1 = S2.
Следователно близо до перихелия на орбитата си планетата се движи най-бързо, а близо до афелия - най-бавно.
По същество вторият закон на Кеплер изразява закон за запазване момента на импулса. Така за двете характерни точки, перихелий и афелий, добива вида:
vп.rп = vа.rа , т.е. от rп < rа ⟹ vп > vа
III. Закон на Кеплер.

където:
а1 и а2 - големи полуоси на орбитите на планетите 1 и 2
Т1 и Т2 - периоди на обикаляне около Слънцето на планетите

𝑀⊙- маса на Слънцето, G = 6.67×10-11 m3/kg.s2 - гравитационна константа.
За планетите в Слънчевата система този закон можем да се запише и в по-опростен вид. Нека положим: а1= a и Т1 = Т за някоя планета, а за Земята да заместим
а2 = 1 AU, a Т2 = 1 yr. Тогава ще се получи третият закон на Кеплер във вида:

Ако се логаритмува под десетичен логаритъм, от последната формула, ще се получи :

т.е. в логаритмична скала се получава правопропорционална зависимост.
Това са приблизителни форми на закона, получени като се има пред вид, че масата на коя да е от планетите m << 𝑀⊙ . В точен вид за две тела с маси m1 и m2, движещи се с период Т около общия си център на масите, законът е:

където a е голямата полуос на орбитата на едно от телата, описвана в координатна система, в която другото тяло се приема за неподвижно.

Ако едно тяло се движи около друго тяло по елипса с голяма полуос a, то неговият период ще бъде един и същ, независимо от това каква е малката полуос на елипсата, т.е. независимо от ексцентрицитета на елипсата. Показаните на фигурата орбити имат различен ексцентрицитет, но еднаква голяма полуос. Орбиталният период е един и същ за тела, движещи се по всяка от тези орбити.
От третия закон на Кеплер следва, че с отдалечаване от Слънцето орбиталните скорости на планетите намаляват, а орбиталните периоди нарастват.
Законите на Кеплер са приложими за планети, спътници на планети, космически апарати, а също така и за двойни звезди и екзопланети.
Исак Нютон извежда и публикува през 1687 г. своя закон за гравитацията като следствие от законите на Кеплер и законите за движението. Обратно, от закона за всеобщо привличане като следствие могат да се изведат трите закона на Кеплер.
Кеплер обяснил как се движат планетите, а Нютон е показал защо те се движат именно така.
* * *
Като илюстрация за прилагане законите на Кеплер може да разгледате следната задача дадена на VIII Национална олимпиада по астрономия (2004 -2005г), Областен кръг, възрастова група 7-8 клас.
5 задача:
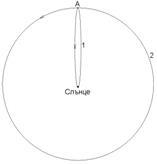
Комета се движи по много силно сплесната орбита около Слънцето (1 -виж фигурата). Земна космическа станция се закрепва към ядрото на кометата. Когато кометата достигне до най-отдалечената точка А от своята орбита, двигателите на станцията се включват за кратко време и в резултат на маневрата кометата тръгва по кръгова орбита около Слънцето (2). Разстоянието от Слънцето до точка А е 100 AU (астрономически единици).
- Докажете, че периодът на кометата по кръговата орбита ще бъде 1000 години.
- Приблизително с колко трябва да се промени скоростта на кометата в точка А, така че тя да тръгне по кръговата орбита?
Ето част от още една задача: XIV Национална олимпиада по астрономия (2010-2011г.), Областен кръг, възрастова група 11-12 клас.
Задача 4. Стационарен спътник
Геостационарен се нарича изкуствен спътник на Земята, който се движи по кръгова орбита точно над Екватора, с период точно равен на периода на околоосно въртене на Земята, и в посоката на това въртене. Така той се намира постоянно над една и съща точка и не се движи видимо по небето.
а) Пресметнете височината на такъв спътник над земната повърхност.
- Ако се нуждаете от справочни данни, потърсете ги в справочник или в интернет.
- При затруднение, потърсете в страницата на олимпиадата тези задача и им разгледайте решенията!
Използвани източници:
Страница на Национална олимпиада по астрономия, раздел „Пищов“, 2004 – 2020г.
Астрономия, Цветан Георгиев, Петко Недялков, Издателство на Нов български университет, София, 2017г.
https://bg.wikipedia.org/wiki/Йохан_Кеплер
https://nauka.offnews.bg/news/Novini_1/Na-27-dekemvri-1571-e-roden-Johan-Kepler-otkrivateliat-na-zakonite-za_66232.html

